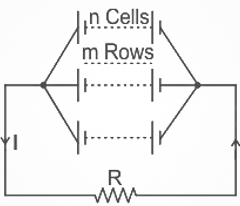
In a parallel series combination of cells, there are m rows and each row contains n cells in series. If r is the internal resistance of each cell and R is the load resistance, what is the condition for maximum power transfer?

In a parallel series combination of cells, there are m rows and each row contains n cells in series. If r is the internal resistance of each cell and R is the load resistance, what is the condition for maximum power transfer?

Right Answer is:

m.R = n. r

SOLUTION

  • There are m rows of cells, with each row containing nn cells connected in series.
  • The internal resistance of each cell is r.
  • The total internal resistance for one row of n cells in series is:

R_internal Resistance = nr.

  • Since there are m such rows connected in parallel, the equivalent internal resistance Req​ of the entire configuration is given by:

Req = R_internal Resistance/m  = nr / m

In a parallel series combination of cells, there are m rows and each row contains n cells in series.

Maximum Power Transfer Condition

According to the Maximum Power Transfer Theorem, maximum power is transferred to the load when the load resistance R is equal to the equivalent internal resistance of the source. Therefore, for maximum power transfer:

R = Req

Substituting for Req

R=n⋅r/m

Rearranging for Conditions

mR=n⋅r

Conclusion

Thus, the condition for maximum power transfer in this configuration is mR=n⋅r

 

Start typing and press enter to search

Scroll to Top