4 से 1 Mux का आउटपुट है
4 से 1 Mux का आउटपुट है
Right Answer is:
$\overline{X+Y}$
SOLUTION
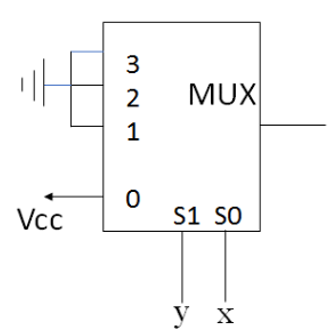
चूंकि 1, 2 और 3 ग्राउंडेड हैं, इसलिए उनके लिए निम्नलिखित मान हैं:
| S1 | S0 | V |
| 0 | 0 | I0 |
| 0 | 1 | I1 |
| 1 | 0 | I2 |
| 1 | 1 | I3 |
I0 = 1
I1 = 0
I2 = 0
I3 = 0
यहाँ $ x = S_2 $ और $ y = S_1 $ हैं।
4×1 मल्टीप्लेक्सर (MUX) का आउटपुट इस प्रकार दिया गया है:
$Y = F = \bar{S_1}\bar{S_2}I_0 + \bar{S_1}S_2I_1 + S_1\bar{S_2}I_2 + S_1S_2I_3$
अब हम मानों को प्रतिस्थापित करते हैं:
$F = \bar{y}\bar{x} \cdot 1 + \bar{y}x \cdot 0 + y\bar{x} \cdot 0 + yx \cdot 0$
सरल करते हुए:
$F = \bar{y}\bar{x}$
यहाँ, $ F = \bar{X}\bar{Y} = \overline{X+Y} $ के रूप में भी लिखा जा सकता है।
इसका अर्थ है कि आउटपुट $ F $ तब ही उच्च (1) होगा जब दोनों इनपुट $ S_1 $ और $ S_2 $ (या $ y $ और $ x $) निम्न (0) होंगे।