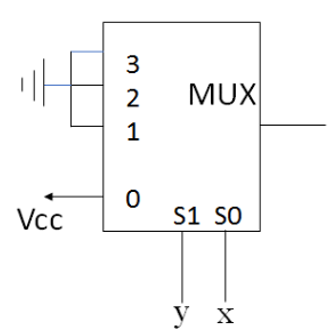
The output of the 4 to 1 Mux is

Question

ITI Exams · Accepted Answer

Since 1, 2 & 3 are grounded.

S1
S0
V

0
0
I0

0
1
I1

1
0
I2

1
1
I3

I0 = 1, I1 = 0, I2 = 0, I3 = 0
x = S2
y = S1
The output of the 4 x 1 MUX is:
$Y = F = \bar{S_1}\bar{S_2}I_0 + \bar{S_1}S_2I_1 + S_1\bar{S_2}I_2 + S_1S_2I_3$
Substituting the values:
$F = xy \cdot 1 + xy \cdot 0 + xy \cdot 0 + xy \cdot 0$
Simplifying:
$F =\bar{X}\bar{Y} = \overline{X+Y}$

The output of the 4 to 1 Mux is

x+ y

x.y

X̄+Ȳ

$\overline{X+Y}$

Right Answer is:
$\overline{X+Y}$

SOLUTION

The output of the 4 to 1 Mux is

x+ y

x.y

X̄+Ȳ

$\overline{X+Y}$

Right Answer is: $\overline{X+Y}$

SOLUTION

Start typing and press enter to search

Right Answer is:
$\overline{X+Y}$